muffin
Constraint Answer Set Programming (CASP) System
Overview
- muffin is the name of both CASP language and solver developed by Haruki Noritake (Kobe University) as a part of the work for his master's thesis.
- muffin language denotes its CASP language.
- muffin solver denotes its CASP solver.
- but we sometimes just call them muffin if there is no confusion.
- This research is supported by "2013 NII Collaborative Research Grants" whose members are:
- Katsumi Inoue (NII)
- Naoyuki Tamura (Kobe University)
- Mutsunori Banbara (Kobe University)
- Torsten Schaub (Potsdam University)
- Takehide Soh (Kobe University)
muffin Language
What about muffin language?
Constraints are written by reserved predicates variable, constraint. Constraints of variable-arguments can also be written by a reserved predicates collection.
- variable(V, int(LB, UB))
- define integer variable V (LB \(\le\) V \(\le\) UB)
- constraint(A)
- define constraint A
- collection(C, X)
- define collection C which collects a variable (or constraint) X.
Which constrains we can use?
Almost all constraints provided by the SAT-based constraint solver Sugar (see the page of syntax of Sugar).
- Arithmetic operator
- abs, neg, add (\(+\)), sub (\(-\)), mul (\(\times\)), mod, min, max
- Comparison operator
- eq (\(=\)), ne (\(\ne\)), le (\(\le\)), lt (\(<\)), ge (\(\ge\)), gt (\(>\))
- Logical operator
- not (\(\neg\)), and (\(\wedge\)), or (\(\vee\)), imp (\(\rightarrow\)), xor (\(\oplus\)), iff (\(\leftrightarrow\)), if
- Global Constraints
- AllDifferent and many more (see syntax of Sugar).
Example1: \(x_1 + x_2 + x_3 + x_4 \le 5\), where \(x_{i} \in \{1, 2, 3\}\)
We write this constraint using variable and constraint.
1: variable(x(1), int(1,3)). 2: variable(x(2), int(1,3)). 3: variable(x(3), int(1,3)). 4: variable(x(4), int(1,3)). 5: 6: constraint(le(add(x(1),x(2),x(3),x(4)),5)) % explicitly write variables in "add".
We can aggregate \(x_1, \ldots, x_4\) into \(xs\) using collection.
1: variable(x(1), int(1,3)). 2: variable(x(2), int(1,3)). 3: variable(x(3), int(1,3)). 4: variable(x(4), int(1,3)). 5: 6: collection(xs, x(1)). 7: collection(xs, x(2)). 8: collection(xs, x(3)). 9: collection(xs, x(4)). 10: 11: constraint(le(add(collection(xs)),5)) % collection(xs) is used instead of "x(1),x(2),x(3),x(4)"
We can further concisely write this program with ASP feature.
1: num(1;2;3;4). 2: variable(x(I), int(1,3)) :- num(I). 3: 4: collection(xs, x(I)) :- num(I). 5: 6: constraint(le(add(collection(xs)),5))
Example2: \(alldifferent(x_1, \ldots, x_{n})\), where \(n=4\) and \(x_{i} \in \{1, \ldots, n\}\)
1: #const n = 4. 2: num(1..n). 3: variable(x(I), int(1,n)) :- num(I). % define variables x_1, ..., x_n 4: 5: collection(xs, x(I)) :- num(I). % define a collection xs which aggregates x_1, ..., x_n 6: 7: constraint(alldifferent(collection(xs))).
muffin Solver Architecture
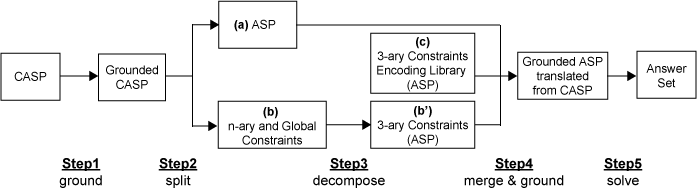
The above figure shows the procedure of the muffin solver. In the following, we domonstrate how it is solved by using Example 2 (alldifferent).
Step 1
The given CASP is grounded into plain text format by gringo.
num(1). num(2). num(3). num(4). variable(x(4),int(1,4)). variable(x(3),int(1,4)). variable(x(2),int(1,4)). variable(x(1),int(1,4)). collection(xs,x(4)). collection(xs,x(3)). collection(xs,x(2)). collection(xs,x(1)). constraint(alldifferent(collection(xs))).
Step 2
The grounded CASP is split into two parts: (a) n-ary and global constraints, (b) ASP.
- (a) ASP
num(1). num(2). num(3). num(4).
- (b) n-ary and global constraints
variable(x(4),int(1,4)). variable(x(3),int(1,4)). variable(x(2),int(1,4)). variable(x(1),int(1,4)). collection(xs,x(4)). collection(xs,x(3)). collection(xs,x(2)). collection(xs,x(1)). constraint(alldifferent(collection(xs))).
Step 3
The part (b) is decomposed by using Sugar.
- Actual implementation does the folloings:
- The input (b) once conveted into Sugar-Prolog format.
- It is then decomposed to 3-ary constraints.
- Finally, it is converted to ASP format (b').
var(x(1)). lb(x(1),1). ub(x(1),4). var(x(2)). lb(x(2),1). ub(x(2),4). var(x(3)). lb(x(3),1). ub(x(3),4). var(x(4)). lb(x(4),1). ub(x(4),4). % the decompotion of alldifferent 1 {le(-1,x(3),1,x(4),-1), ge(-1,x(3),1,x(4),1)}. 1 {le(-1,x(2),1,x(4),-1), ge(-1,x(2),1,x(4),1)}. 1 {le(-1,x(1),1,x(4),-1), ge(-1,x(1),1,x(4),1)}. 1 {le(-1,x(2),1,x(3),-1), ge(-1,x(2),1,x(3),1)}. 1 {le(-1,x(1),1,x(3),-1), ge(-1,x(1),1,x(3),1)}. 1 {le(-1,x(1),1,x(2),-1), ge(-1,x(1),1,x(2),1)}. % hint: pigeon hole constraints for alldifferent generated by Sugar 1 {ge0(1,x(4),4), ge0(1,x(3),4), ge0(1,x(2),4), ge0(1,x(1),4)}. 1 {le0(1,x(4),1), le0(1,x(3),1), le0(1,x(2),1), le0(1,x(1),1)}.
Step 4
The three parts, (a), (b'), (c) 3-ary constraints encoding library, are grounded by gringo.
- We use oe.lp in salt for (c), which adopts order encoding.
Step 5
An answer set obtained by clasp is as follows.
p(x(1),4) p(x(1),3) % x_{1} = 3
p(x(2),4) p(x(2),3) p(x(2),2) % x_{2} = 2
p(x(3),4) p(x(3),3) p(x(3),2) p(x(3),1) % x_{3} = 1
p(x(4),4) % x_{4} = 4
Implementations of muffin
We currently have two implementation variants of muffin.
muffin (original)
- Requirements – following commands are necessary to be installed.
- glingo
- clasp
- swipl
- egrep
- perl
- sugar: version 2.1.3
- Instalation
- download muffn.tar.gz
- uppack.
- How to run.
$ cd muffin $ ./muffin.sh examples/magic_square.lp
mfn
More or less, batch program (written in Scala) executing each step.
Both "casp" and "xcsp" can be solved.
- Requirements – following commands are necessary to be installed.
- glingo
- clasp
- swipl
- sugar: version 2.1.3
- scala: version 2.10.*
- Installation
- download mfn.tar.gz
- unpack.
- How to run.
$ cd mfn $ ./mfn examples/alldiff.lp
- Available Options
Usage: ./mfn [options] [inputFile] -no_simp off Tseitin translation in Sugar -keep keep all temporal files -xcsp accept xcsp format -C<clasp options> any clasp options -G<gringo options> any gringo options in Step5 Ex1. enumerate all answer sets without display. with clasp stats. no Tseitin translation. $ ./mfn -C-n 0 -C--quiet -C-s -no_simp examples/alldiff.lp Ex2. solve xcsp with "jumpy". print gringo stats. keep temporal files. $ ./mfn -xcsp -G--gstats -C--configuration=jumpy -keep examples/queens-12.xml
- Output Examples (download).
salt
salt is an ASP-based CSP solver.
More Examples of muffin
Magic Square
- Example of Magic Square.
- All outputs of mfn.jar for this example is available here.
#const n = 3. #const sum = n*(n*n+1)/2. num(1..n). line(row(I)) :- num(I). line(col(J)) :- num(J). line(d1;d2). variable(x(I,J), int(1,n*n)) :- num(I), num(J). collection(xs, x(I,J)) :- num(I), num(J). collection(row(I), x(I,J)) :- num(I), num(J). collection(col(J), x(I,J)) :- num(I), num(J). collection(d1, x(I,I)) :- num(I). collection(d2, x(I,n-I+1)) :- num(I). constraint(alldifferent(collection(xs))). constraint(eq(add(collection(L)), sum)) :- line(L).
Knapsack problem
- The following muffin program shows a knapsack problem instance of this table.
- All outputs of mfn.jar for this example is available here.
| Items | book | shirt | note | passport | pc |
|---|---|---|---|---|---|
| Weight | 3 | 3 | 1 | 1 | 5 |
| Value | 2 | 3 | 3 | 5 | 5 |
#const ub_weight = 9. #const lb_value = 13. item(book, 3, 2). item(shirt, 3, 3). item(note, 1, 3). item(passport, 1, 5). item(pc, 5, 5). variable(x(Item), int(0,1)) :- item(Item, Price, Value). collection(prices, mul(Price,x(Item))) :- item(Item, Price, Value). collection(values, mul(Value,x(Item))) :- item(Item, Price, Value). constraint(le(add(collection(prices)), ub_weight)). constraint(ge(add(collection(values)), lb_value)).
Implementations and Publications of other CASP systems.
Download bibtex file of the following papers.
Surveys etc.
- Yuliya Lierler. Relating constraint answer set programming languages and algorithms, Artificial Intelligence, Volume 207, pp. 1–22, 2014.
- Yuliya Lierler. Constraint answer set programming. ALP newsletter feautured article, 2012.
- S. Baselice, P.A. Bonatti, and M. Gelfond. Towards an integration of answer set and constraint solving. In Maurizio Gabbrielli and Gopal Gupta, editors, Logic Programming, volume 3668 of Lecture Notes in Computer Science, pages 52–66. Springer Berlin Heidelberg, 2005.
Translational Approach
- asparatame (Translate CSP to ASP)
- Mutsunori Banbara, Martin Gebser, Katsumi Inoue, Torsten Schaub, Takehide Soh, Naoyuki Tamura, and Matthias Weise. Aspartame: Solving constraint satisfaction problems with answer set programming. CoRR, abs/1312.6113, 2013.
- MINGO (Translate CASP to MIP)
- Guohua Liu, Tomi Janhunen, and Ilkka Niemela. Answer set programming via mixed integer programming. In Proceedings of the 13th International Conference (KR'12), 32—42, Rome, Italy, June 2012. AAAI Press.
- inca (Translate CASP to ASP)
- Christian Drescher and TobyWalsh. A translational approach to constraint answer set solving. TPLP, 10(4-6):465–480, 2010.
- Christian Drescher and Toby Walsh. Translation-based constraint answer set solving. In IJCAI, pages 2596–2601, 2011.
- xpanda (Translate CASP to ASP)
- Martin Gebser, Henrik Hinrichs, Torsten Schaub, and Sven Thiele. xpanda: A (simple) preprocessor for adding multi-valued propositions to ASP, 2009.
- ezcsp (Translate CASP to CSP)
- Marcello Balduccini. Representing constraint satisfaction problems in answer set programming. In In: ICLP09 Workshop on Answer Set Programming and Other Computing Paradigms (ASPOCP09), 2009.
- IDP (Translate first order logic with numerical costraints to SAT)
- Johan Wittocx, Maarten Marien, and Marc Denecker. The IDP system: a model expansion system for an extension of classical logic. In Logic And Search (Lash), 2008.
Hybrid (SMT-like) Approach
- clingcon (clingo + gecode)
- Martin Gebser, Max Ostrowski, and Torsten Schaub. Constraint answer set solving. In ICLP, pages 235–249, 2009.
- Max Ostrowski and Torsten Schaub. Asp modulo csp: The clingcon system. TPLP, 12(4-5):485–503, 2012.
- acsolver (Smodels + Sicstus Prolog)
- VeenaS. Mellarkod, Michael Gelfond, and Yuanlin Zhang. Integrating answer set programming and constraint logic programming. Annals of Mathematics and Artificial Intelligence, 53(1-4):251–287, 2008.